What is a graph?
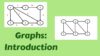
A graph is a collection of nodes (also called vertices) connected to each other through edges. For example, the below figure is a graph with 6 vertices and 9 edges.

Mathematically, Graph G is an ordered pair of V vertices and E edges, ie. G = (V,E).
An edge from a vertex a to vertex b is an ordered pair (a,b) if there is a directed edge between the two and an unordered pair {a,b} if there is an undirected edge between the two.
A directed edge between a and b means we can move from a to b only and never from b to a. An undirected edge between a and b means we can go from a to b and also from b to a.
The above graph has only the undirected edges between its vertices.
The vertices set V of above graph will be:
V = { 1, 2, 3, 4, 5, 6}
And the edges set E will be:
E = { {1, 2}, {1, 5}, {1, 4}, {2, 3}, {2, 5}, {2, 6}, {3, 6}, {4, 5}, {5, 6} }
Now, Let’s consider an example of a graph with directed edges and write it’s set V and set E.

The set of vertices will be same:
V = { 1, 2, 3, 4, 5, 6}
But the set of edges will differ:
E = { (1, 2), (1, 5), (1, 4), (1, 6), (2, 3), (3, 6), (4, 5), (5, 6) }
Directed and Undirected Graphs
A directed graph is a graph which has directed edges while an undirected graph is a graph which has only undirected or bi-directional edges. For example, Fig 1 is an undirected graph and Fig 2 is a directed graph.
Weighted and Un-Weighted graph
If there is a cost/weight associated with all edges in a graph, then that graph is a weighted graph. If there is no weight associated with the edges like in Fig 1 and Fig 2, then it is an un-weighted graph. Fig 3 is a weighted graph where edges have a weight of 5, 10 or 15 associated with them.

In the next post, we will implement graphs in Java and perform operations on them.
2 responses to “Graphs: Introduction”
Quick and handy refresher for Graphs concepts. Thanks
You are welcome 🙂